オントロジーにおける推論

「推論」はオントロジーにおける最重要テーマの１つで、リンクトデータで記述されている概念間の関係性では述べられていない部分に関して推論を行うことで、より多くの情報を扱う事ができ、セマンティックWebで多種多様なデータの関係性を表現する事ができるようになります。

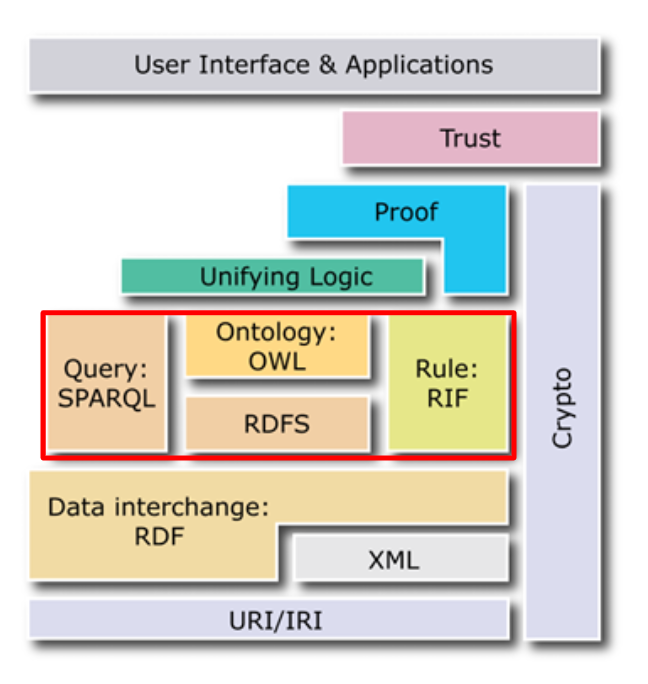
セマンティックWebのレイヤーケーキ上では、RDFS、OWL、SPARQL、RIF等がオントロジーの推論に該当する構成要素で、これらに共通して用いられる推論の概念についての解説をさせて頂きます。

 

記述論理

オントロジーにおける推論を説明する際に、記述論理（description logic: DL　※以下DLと記述）という知識表現のための記述方法について説明を行っておく必要があります。DLは概念が複雑なため、オントロジーやセマンティックWebの概要を知りたいという方は深入りせず、流し読みをして頂く程度で良いかと思います。まず、DLの全体像を表現すると、大まかに以下の図のようになります。

この図を見ても、DLの概念は複雑なため、直感的に理解する事は難しいと思います。以下、詳細を別個に解説していきます。

DLのシンタクスについて

DLが知識表現のための記述方法である事は既に述べた通りですが、DLで知識を表現する際に用いられるシンタクスについて精鋭をしたものが、上の図の左半分の部分（「概念言語」）です。各シンタクスの構成要素は以下のようになります。

• 概念名：知識表現の対象とする概念の名前、オントロジーの概念に対応
• ロール名：概念間の関係性についての定義、オントロジーのプロパティに対応
• 実態名：概念に属する個体の名前、オントロジーの個体に対応
• コンストラクタ：概念間の関係性を定義するための記述式、∏（共通）, ∐（結合）, ¬（補元）, ∀（存在制限）, ∃（制限値）で構成され、これらを組み合わせて複雑な概念の表現が可能

上記のDLのシンタクスを用いることにより、概念間の複雑な関係の記述が可能になります。上の図の複雑な概念の記述例の意味は以下となります。

• Human ∏ Male：Human（人間で）とMale（男性）の共通概念なので、人間の男性を表している
• Human ∏ ∃hasChild.Human：Human（人間）とhasChild.Human（子供がいる人間という制限）の共通要素なので、子供がいる人間を表している

このように、シンタクスを用いて、オントロジーの複雑な概念を記述する事が出来ます。

知識ベース（DL）

上の図の右上の部分にあたる、知識ベース（Knowledge Base:KB　以下、KBと記述）についての解説を進めていきます。KBはTBox、及びABoxから構成され、それぞれ以下のような役割をもっています。

• TBox：概念記述と呼ばれ、オントロジーにおける概念（クラス）に相当する
• ABox：個体記述と呼ばれ、オントロジーにおける個体（インスタンス）に相当する

つまり、上述のシンタックスを用いて、クラス、及びインスタンスに関する概念を記述したものをまとめておく保管庫にあたるのがKBと言えます。このKBは次に解説する「推論」に用いられます。

推論

冒頭でもお話をした通り、オントロジーにおいて推論は、概念間の関係性を正しく把握する上で非常に重要な要素です。また、オントロジーはDLで記述する事ができ、DLは論理システムなので推論を行うことができます。推論は具体的には以下のような内容になります。

• 充足性チェック：KBに「TBox」モデルがあるかを確認
• インスタンスチェック：実体aが、概念Cのインスタンスかどうか、C(a)のモデルがあるかを確認
• 概念充足性チェック：概念Cのモデルがあるかを確認
• 概念包含チェック：概念Cが、概念Dに包含されるか（C⊆D）確認

次に、推論のアルゴリズムの中で有名なタブロー法という推論法の解説をさせて頂きます。

 

タブロー法

タブローとはフランス語で表の事を指し、ある命題の正しさを証明する帰納法により立証する方法として有名な方法です。タブロー法の詳細は数学的な話になるため、以下概念のみ簡単に説明いたします。タブローによる命題の証明は以下の手順で行われます。

1. 命題の否定標準形（NNF）の生成
2. タブローの拡張規則の展開
3. タブローが閉じるかの確認

命題の否定標準形（NNF）の生成

タブロー法による命題証明の最初のステップは、命題を否定標準形（NNF）に変換する事です。NNFは命題の先頭を否定形にすることで表現され、以下がNNFの一例になります。

タブローの拡張規則の展開

NNFに変換した命題を、タブローの拡張規則という規則で、木構造に展開を行います。以下が拡張規則の一覧となります。この規則をNNFに展開していき、それ以上展開できなくなるまで展開を進めます。

タブローが閉じるかの確認

拡張規則を展開していき、それ以上展開が出来なくなった時点で、タブローが閉じたかどうかの確認を行います。タブローが閉じたかどうかは、命題の各要素のクラッシュ（クラッシュとは例えば、A₀と￢A₀の対を指す）が生成されたかどうかで確認が出来ます。

また、タブローが閉じるとその命題は恒真となり、その命題が恒真であればタブローが閉じるという関係性があります。これを下の図のように、タブローの健全性と完全性と言います。

 

まとめ

オントロジー中でも推論は非常に大事な要素で、複雑な概念を記述するために用いられるDLの紹介と、推論を行うことにより、概念間の関係性や、命題の正しさなどを立証する事ができ、これにより高度なセマンティックWebの表現を実現できるようになります。

推論はセマンティックWebのレイヤーケーキ上では、RDFの上位に位置するRDFS、OWL、SPARQL、RIF等の構成要素で用いられます。次回以降はこれらの構成要素の詳細を解説いたします。